Section 3 Guidance for calculations

3.1.1 The basic principle is that the alternating working stresses shall be below the local fatigue strength (including the effect of surface treatment) wherein non-propagating cracks may occur, see also Ch 3, 6.1 Cold forming general comments for details. This is then divided by a certain safety factor. This applies through the entire fillet or oil bore contour as well as below the surface to a depth below the treatment-affected zone, i.e. to cover the depth all the way to the core.

3.1.2 Consideration of the local fatigue strength shall include the influence of the local hardness, residual stress and mean working stress. The influence of the ‘giga-cycle effect’, especially for initiation of subsurface cracks, should be covered by the choice of safety margin.

3.1.3 It is of vital importance that the extension of hardening/peening in an area with concentrated stresses be duly considered. Any transition where the hardening/peening is ended is likely to have considerable tensile residual stresses. This forms a ‘weak spot’ and is important if it coincides with an area of high stresses.

3.1.5 The acceptability criterion should be applied stepwise from the surface to the core as well as from the point of maximum stress concentration along the fillet surface contour to the web.

3.2.1 It is necessary to have knowledge of the stresses along the fillet contour as well as in the subsurface to a depth somewhat beyond the hardened layer. Normally this will be found via FEA as described in Ch 1 Guidance for Calculation of Stress Concentration Factors in the Web Fillet Radii of Crankshafts Through the Utilisation of the Finite Element Method. However, the element size in the subsurface range must be the same size as at the surface. For crankpin hardening, only the small element size will have to be continued along the surface to the hard layer.

3.2.2 If no FEA is available, a simplified approach may be used. This can be based on the empirically determined stress concentration factors (SCFs) from the ‘Stress concentration factors’ sub-section of the applicable Rules, if within its validity range, and a relative stress gradient inversely proportional to the fillet radius.

3.2.3 Bending and torsional stresses must be addressed separately. The combination of these is addressed by the acceptability criterion.

3.2.4 The subsurface transition-zone stresses, with the minimum hardening depth, can be determined by means of local stress concentration factors along an axis perpendicular to the fillet surface. These functions, α_B-local and α_T-local, have different shapes due to the different stress gradients.

3.2.5 The SCFs α_B and α_T are valid at the surface. The local α_B-local and α_T-local drop with increasing depth. The relative stress gradients at the surface depend on the kind of stress raiser, but for crankpin fillets they can be simplified to 2/R_H in bending and 1/R_H in torsion. The journal fillets are handled analogously by using R_G and D_G. The nominal stresses are assumed to be linear from the surface to a midpoint in the web between the crankpin fillet and the journal fillet for bending, and to the crankpin or journal centre for torsion.

3.2.6 The local SCFs are then functions of depth t according to equation as shown in Figure 3.3.2 Bending SCF in the crankpin fillet as a function of depth for bending, and according to equation as shown in Figure 3.3.3 Torsional SCF in the crankpin fillet as a function of depth for torsion.

3.2.7 The corresponding SCF for the journal fillet can be found by replacing R_H with R_G for bending and by replacing R_H with R_G and D with D_G for torsion.

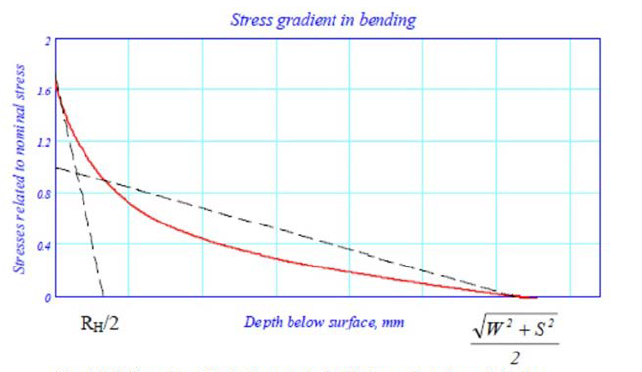
Figure 3.3.2 Bending SCF in the crankpin fillet as a function of depth

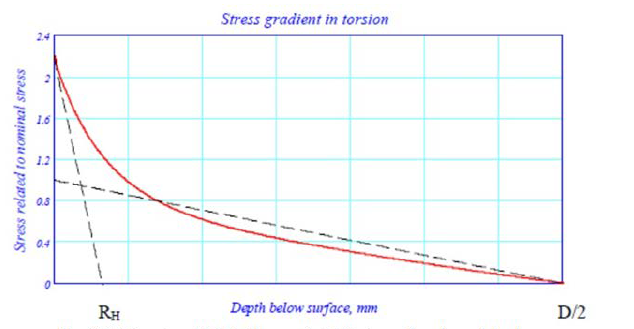
Figure 3.3.3 Torsional SCF in the crankpin fillet as a function of depth

3.2.8 If the pin is hardened only and the end of the hardened zone is closer to the fillet than three times the maximum hardness depth, FEA should be used to determine the actual stresses in the transition zone.

3.3.1 Stresses in the oil bores can be determined also by FEA. The element size should be less than 1/8 of the oil bore diameter D_O and the element mesh quality criteria should be followed as prescribed in Ch 4 Guidance for Calculation of Stress Concentration Factors in the Oil Bore Outlets of crankshafts through utilisation of the Finite Element Method. The fine element mesh should continue well beyond a radial depth corresponding to the hardening depth.

3.3.2 The loads to be applied in the FEA are the torque – see Ch 1, 3.2 Torsion – and the bending moment, with four-point bending as in Ch 1, 3.3 Pure bending (4 point bending).

3.3.4 Figure 3.3.4 Stresses and hardness in induction hardened oil holes indicates a local drop of the hardness in the transition zone between a hard and soft material. Whether this drop occurs also depends on the tempering temperature after quenching during the QT process.

3.3.5 The peak stress in the bore occurs at the end of the edge rounding. Within this zone, the stress drops almost linearly to the centre of the pin. As can be seen from Figure 3.3.4 Stresses and hardness in induction hardened oil holes, for shallow (A) and intermediate (B) hardening, the transition point practically coincides with the point of maximal stresses. For deep hardening, the transition point comes outside of the point of peak stress and the local stress can be assessed as a portion (1-2t_H/D) of the peak stresses where t_H is the hardening depth.

3.3.6 The subsurface transition-zone stresses (using the minimum hardening depth) can be determined by means of local stress concentration factors along an axis perpendicular to the oil bore surface. These functions, γ_B-local and γ_T-local, have different shapes because of the different stress gradients.

3.4.1 Acceptance of crankshafts is based on fatigue considerations; the applicable Rules compare the equivalent alternating stress and the fatigue strength ratio to an acceptability factor of Q ≥ 1,15 for oil bore outlets, crankpin fillets and journal fillets. This shall be extended to also cover surface treated areas, independent of whether surface or transition zone is examined.