Section 4 Design criteria

4.1.1 The allowable stress, σ_a, is to be taken as the failure stress of the component concerned multiplied by a stress factor, F, which depends on the load case considered. The allowable stress is given by the general expression:

4.1.2 The stress factors, F, for steels in which

are given in Table 5.4.1 Stress factor, F.

4.1.3 For steel with the allowable stress is to be derived from the following expression:

4.1.4 The failure stress for the elastic modes of failure are given in Table 5.4.2 Failure stress.

4.1.5 For components subjected to combined stresses the following allowable stress criteria are to be used:

1. σ_xx < Fσ_t

2. σ_yy < Fσ_t

3. τ_o < Fτ

4. σ = (σ_xx ² + σ_yy ² - σ_xx σ_yy + 3τ_o ²)^1/2 ≤ 1,1Fσ_t

4.2.1 The allowable axial stress for compression members is to be taken as the critical compressive stress, σ_cr, multiplied by the allowable stress factor, F, as defined in Table 5.4.1 Stress factor, F.

4.2.2 For members subjected to simple compression the critical compression stress is given by the Perry-Robertson formula below:

where

σe	=
η	=
E	=	Young's modulus, in N/mm2
l	=	length in mm
r	=	radius of gyration, in mm
a	=	Robertson's constant as per Table 5.4.3 Values of Robertson Constant, a, for various sections
σy	=	yield stress, in N/mm2
K	=	constant dependant on the end constraint condition of the member as per Table 5.4.4 Value K, for different constraint conditions.

4.2.3 For members subjected to combined bending and compression the following stress criteria are to be used:

4.3.1 The allowable stress is to be taken as the critical buckling stress σ_cb, σ_bb, or τ_b as appropriate of the component concerned multiplied by the stress factor, F, as defined in Table 5.4.1 Stress factor, F.

4.3.2 For components subject to compression the critical buckling stress is given by:

1. for σ_cb < 0,5σ_y

   

2. for σ_cb ≥ 0,5σ_y

   

Kc

=

compression buckling constant, defined as follows for α ≥ 1: for α < 1: where α = μ = Poisson’s ratio a = plate length, i.e. in the direction of stress The graphical representation of Kc is provided in Figure 5.4.1 Compression buckling constant Kc.

4.3.3 For components subject to shear, the critical buckling stress is given by:

1. for τ_b < 0,29σ_y

   

2. for τ_b ≥ 0,29σ_y

   

where

τb	=	critical shear buckling stress, in N/mm2
σy	=	yield stress, in N/mm2
E	=	Young's modulus, in N/mm2
t	=	plate thickness, in mm
b	=	smallest plate dimension, in mm.
Ks	=	shear buckling constant, defined as follows for α ≥ 1: for α < 1: where α = μ = Poisson’s ratio a = plate length corresponding to b The graphical representation of Ks is provided in Figure 5.4.2 Shear buckling constant Ks.

4.3.4 For components subject to bending stress the critical buckling stress is given by:

1. for σ_bb < 0,5σ_y

   

2. for σ_bb ≥ 0,5σ_y

   

where

σbb	=	critical buckling stress, in N/mm2
σy	=	yield stress, in N/mm2
E	=	Young's modulus, in N/mm2
t	=	plate thickness, in mm
b	=	plate width, i.e. normal to direction of stress, in mm.
Kb	=	bending buckling constant, defined as follows for α ≥ : for α < : where α = μ = Poisson’s ratio a = plate length, i.e. in the direction of stress The graphical representation of Kb is provided in Figure 5.4.3 Bending buckling constant Kb.

4.3.5 For components subject to combined compression and shear, the following allowable stress criteria are to be met:

1. σ_c < Fσ_cb

2. τ < Fτ_b

3. 

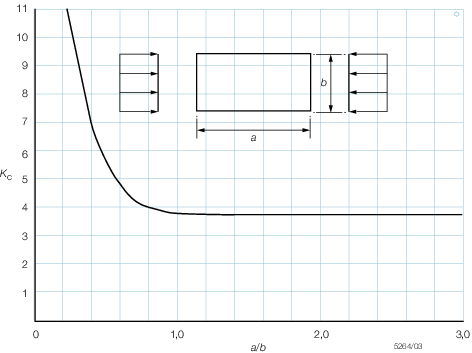
Figure 5.4.1 Compression buckling constant Kc

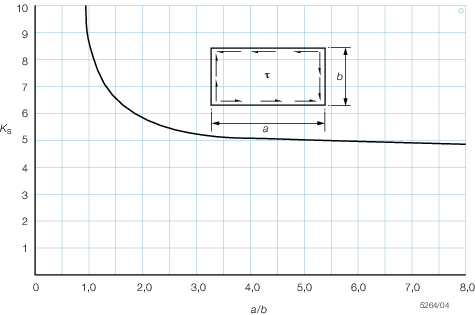
Figure 5.4.2 Shear buckling constant Ks

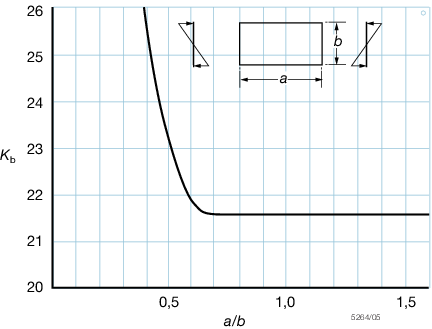
Figure 5.4.3 Bending buckling constant Kb

4.3.6 For components subject to combined bending and shear, the following stress criteria are to be met:

1. σ_b < Fσ_bb

2. τ < Fτ_b

3. 

Table 5.4.4 Value K, for different constraint conditions

Diagramatic representation	Restraint conditions	K
	Constrained against rotation and translation at both ends	0,7
	Constrained against rotation and translation at one end and translation only at other end	0,85
	Constrained against translation only at each end	1,0
	Constrained against rotation and translation at one end and against rotation only at other end	1,5
	Constrained against rotation and translation at one end and free to rotate and translate at other end	2,0

4.3.7 For components subject to combined bending and compression the following allowable stress criteria are to be met:

1. σ_c < Fσ_cb

2. σ_b < Fσ_bb

3. 

4.3.8 For components subject to combined compression, bending and shear, the following allowable stress criteria are to be met:

1. σ_c < Fσ_cb

2. σ_b < Fσ_bb

3. τ < Fτ_b

4. 

4.4.1 For welded joints, the physical properties of the weld metal are considered as equal to the parent metal. For full penetration butt welds, the allowable stress is equal to the allowable stress of the parent material (see Pt 3, Ch 5, 4.1 Allowable stress - Elastic failure).

4.4.2 For fillet welds and welds subjected to shear, the allowable stresses are reduced. Values of these reduced stresses are given in Table 5.4.5 Allowable stresses in welds, N/mm2. Where, F, is the stress factor, see Table 5.4.1 Stress factor, F.

4.4.3 The design stress in fillet welds is to be calculated on the `throat' dimension of the weld. See Figure 5.4.4 Fillet weld dimensions.

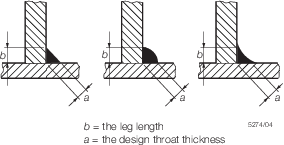
Figure 5.4.4 Fillet weld dimensions

4.4.4 The strength of joints using pretensioned bolts to transmit shear and/or tensile forces, e.g. high strength friction grip bolts, is to be determined in accordance with an appropriate National or other acceptable code or standard.

4.4.5 For joints using precision bolts, defined as turned or cold finished bolts fitted into drilled or reamed holes whose diameter is not greater than the bolt diameter by more than 0,4 mm, the allowable stress due to the externally applied load is given in Table 5.4.6 Allowable stresses for fitted bolts.

4.4.6 Where joints are subjected to fluctuating or reversal of load across the joint the bolts are to be pretensioned by controlled means to between 70 and 80 per cent of their specified yield stress.

Table 5.4.6 Allowable stresses for fitted bolts

Type of loading	Allowable stress
	Load cases	Load case
	1 and 3	2
Tension	0,4 σy	0,54 σy
Single shear	0,38 σy	0,51 σy
Double shear	0,57 σy	0,77 σy
Tension and shear	0,48 σy	0,64 σy
Bearing	0,9 σy	1,2 σy

4.4.7 Black bolts (ordinary grade bolts) are not to be used for primary joints or joints subject to fatigue.

4.5.1 The deck plating thickness, t, for bridges and ramps is to be adequate for the intended vehicle traffic and is to be calculated with reference to the method described in Pt 3, Ch 4, 3.3 Deck plating.

4.5.2 In addition to accommodating the local tyre print loads, the deck plating may also contribute to the overall strength of the bridge or ramp and therefore is to satisfy the allowable stress criteria of Pt 3, Ch 5, 4.1 Allowable stress - Elastic failure and the plate buckling requirements in Pt 3, Ch 5, 4.3 Allowable stress - Plate buckling failure.

4.6.1 In Case 1 the deflection of the bridge or ramp between supports under the applied load is to be limited to that given by the following expression:

4.6.2 For cantilevered sections of bridges and ramps the deflection is to be limited to mm

4.7.1 Where chains are used as part of the hoisting or slewing arrangement they are to have a minimum safety factor of 4,0.

4.7.2 Where wire ropes are used as part of the hoisting or slewing arrangement the safety factor is to be determined as:

The actual design safety factor is to be not less than four and need not be greater than five.

4.8.1 Where bridges and ramps are raised or lowered in the unloaded condition and then pinned or locked off to support both the dead weight and vehicle loads, the pins (or locking device) are to be adequate for the worst loading derived from Case 1 and are to satisfy the allowable stress criteria of Pt 3, Ch 5, 4.1 Allowable stress - Elastic failure,Pt 3, Ch 5, 4.2 Allowable stress - Compression and bending members ,Pt 3, Ch 5, 4.3 Allowable stress - Plate buckling failure ,Pt 3, Ch 5, 4.4 Allowable stress - Joints and connections.

4.9.1 Where a bridge or ramp is retained in position by a single articulated mechanical connection a suitable means is to be provided to prevent the complete detachment of the bridge or ramp from the support in the event of failure of the joint.

4.9.2 Chains or wire ropes used for this purpose are to take due account of the kinetic energy developed by the falling structure and are to have a safety factor of at least two.

4.9.3 To prevent movement and consequent failure, pins for all primary hinges and articulations are to be locked in position by adequate keep plates, castellated and wired nuts, end cover plates or other suitable means.

4.10.1 The gradients of bridges and ramps are in general not to exceed a slope of 1 in 10 during normal operation with ships at lowest or highest freeboard at Mean Low or High Water Spring Tides respectively. Additionally, a maximum slope of 1 in 8 will be permitted for Lowest and Highest Astronomical Tides.

4.10.2 Changes in bridge or ramp gradients and transitions are to take account of ground clearance of the vehicles using the linkspan throughout the operational range.