Section 5 Nitriding

5.1.1 The hardness specification shall include the surface hardness range (minimum and maximum) and the minimum and maximum depth. Only gas nitriding is considered. The referenced Vickers hardness is considered to be HV0.5.

5.1.2 The depth of the hardening is defined in different ways in the various standards and the literature. The most practical method to use in this context is to define the nitriding depth t_N as the depth to a hardness of 50 HV above the core hardness.

5.2.1 It is important to note that in nitrided crankshaft cases, fatigue is found either at the surface or at the transition to the core. This means that the fatigue strength can be determined by tests as described in Ch 2 Guidance for Evaluation of Fatigue Tests.

5.2.2 Alternatively, the surface fatigue strength (principal stress) can be determined empirically and conservatively as:

This is valid for a surface hardness of 600HV or greater:

Note that this fatigue strength is assumed to include the influence of the surface residual stress and applies for a working stress ratio of R = -1.

5.2.3 The fatigue strength in the transition-zone can be determined by the equation introduced in the ‘Fatigue strength’ sub-section of the applicable Rules. For crankpin and respectively to journal the following applies:

	where
		Y = DG	and	X = RG		for journal fillet
		Y = D	and	X = RH		for crankpin fillet
		Y = D	and	X = DO/2		for oil bore outlet

Note that this fatigue strength is not assumed to include the influence of the residual stresses.

5.2.4 In contrast to induction-hardening, the nitrided components have no such distinct transition to the core. Although the compressive residual stresses at the surface are high, the balancing tensile stresses in the core are moderate because of the shallow depth. For the purpose of analysis of subsurface fatigue, the disadvantage of tensile residual stresses in and below the transition zone may even be disregarded in view of this smooth contour of a nitriding hardness profile.

5.2.5 Although in principle the calculation should be carried out along the entire hardness profile, it can be limited to a simplified approach of examining the surface and an artificial transition point. This artificial transition point can be taken at the depth where the local hardness is approximately 20 HV above the core hardness. In such a case, the properties of the core material should be used. This means that the stresses at the transition to the core can be found by using the local SCF formulae in Ch 3, 5.1 Nitriding general comments 5.1.3, inserting t=1,2t_N.

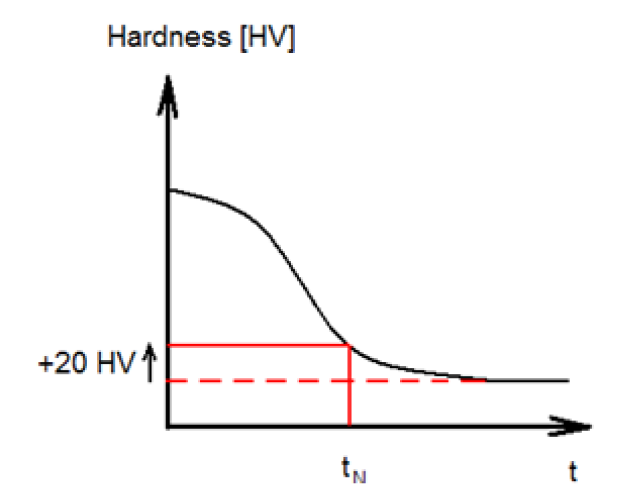
Figure 3.5.1 Sketch of the location for the artificial transition point in the depth direction