1 Tank barge example
Clasification Society 2024 - Version 9.40
Statutory Documents - IMO Publications and Documents - Resolutions - Marine Environment Protection Committee - Resolution MEPC.122(52) - Explanatory Notes on Matters Related to the Accidental Oil Outflow Performance under Regulation 23 of the Revised MARPOL Annex I - (Adopted on 15 October 2004)Amended by Resolution MEPC.146(54) - Annex - Explanatory Notes on Matters Related to the Accidental Oil Outflow Performance under Regulation 23 of the Revised MARPOL Annex I - Part C - Examples - 1 Tank barge example

1 Tank barge example

  1.1 General

  • 1.1.1 The application of the Accidental Oil Outflow Performance regulation is shown in the following worked example illustrating the calculation procedure for a tank barge.

  • 1.1.2 The arrangement and dimensions of the sample barge are as shown figure 26. For clarity purposes, a simple arrangement has been selected which does not comply with all MARPOL requirements. However, for actual designs, the vessel must satisfy all applicable regulations of MARPOL Annex I.

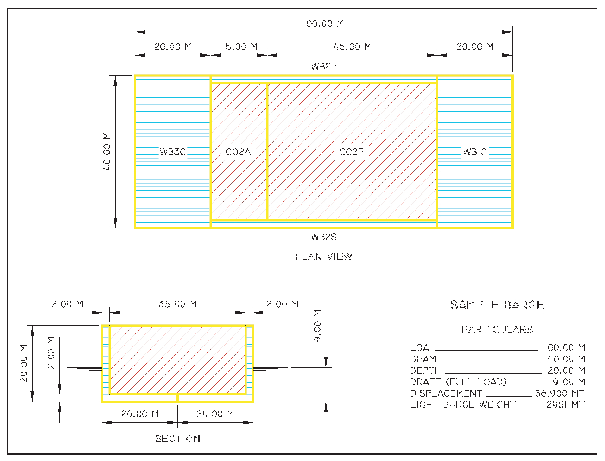
Barge Arrangement

  1.2 Establishing the nominal cargo oil density

  • 1.2.1 The deadweight (DW) equals the displacement at the summer load line draft measured in seawater with a density of 1.025 t/m3 minus the lightship. No deduction is taken for consumables.

  • 1.2.2 The cargo volume C equals the total cargo volume at 98% filling. In accordance with paragraph 4.5 of regulation 23, the capacity of cargo tanks are calculated based on a permeability of 0.99.

      100% Capacity
    (m3)     		98% Filling
    (m3)
    CO1 9,623 9,430
    CO2 28,868 28,291
      C= 37,721

  • 1.2.3 In accordance with paragraph 4.4 of regulation 23, the nominal density is calculated as follows:

    		(1.2.3)

  1.3 Calculating the probabilities of side damage

  • 1.3.1 The first step is to determine the values for the dimensions and clearances Xa, Xf, Zl , Zu and y as defined in paragraph 8.2 of regulation 23:

    Tank Xa
    m-AP     		Xf
    m-AP     		Zl
    m-BL     		Zu
    m-BL     		y
    m
    CO1 20.000 35.000 2.000 20.000 2.000
    CO2 35.000 80.000 2.000 20.000 2.000
               

  • 1.3.2 From the ratios Xa/L, Xf/L, Z/Bs, Zl/Ds, Zu/Ds, Yl/Ds, and y, the probabilities associated with these subdivision locations are interpolated from the table of probabilities for side damage provided in Paragraph 8.3 of regulation 23. For instance, for compartment CO1, the forward boundary Xf is at 35.0 m from the A.P, and Xf/L = 0.35. From the table, we find that Psf = 0.617. The probabilities for CO1 and CO2 are as follows:

    Tank Xa/L PSa Xf/L PSf Zl/DS PSl Zu/DS Psu y/Bs Psy
    CO1 0.2000 0.1670 0.3500 0.6170 0.1000 0.0010 0.1000 0.0000 0.0500 0.7490
    CO2 0.3500 0.3170 0.8000 0.1670 0.1000 0.0010 0.1000 0.0000 0.0500 0.7490
                         

  • 1.3.3 In accordance with paragraph 8 of regulation 23, the probability factors are then combined to find the probability, Ps, of breaching a compartment from side damage.

    • For tank CO1:

      PSL = (1 - Psf - Psa) = (1 - 0.617 - 0.167) = 0.216

      PSV = (1 - Psu - Psl) = (1 - 0.000 - 0.001) = 0.999

      PST = (1 - Psy) = (1 - 0.749) = 0.251

      Ps = PSL PSV PST = (0.216)(0.999)(0.251) = 0.0542

    • For tank CO2:

      PSL = (1 - Psf - Psa) = (1 - 0.167 - 0.317) = 0.516

      PSV = (1 - Psu - Psl) = (1 - 0.000 - 0.001) = 0.999

      PST = (1 - Psy) = (1 - 0.749) = 0.251

      Ps = PSL PSV PST = (0.216)(0.999)(0.251) = 0.1294

  • 1.3.4 Given a collision that penetrates the outer hull, Ps is the probability that the damage will extend into a particular cargo tank. As shown above, the probability of breaching the CO2 tank from side damage is 0.1294, or about 12.9%.

  1.4 Calculating the mean outflow from side damage

  • 1.4.1 For side damage, the total content of the tank is assumed to outflow into the sea when the tank is penetrated. Thus, the mean outflow is calculated by summing the products of the cargo tank volumes at 98% filling and the associated probabilities, in accordance with the formula given in paragraph 6 of regulation 23:

    		(1.4.1)

  • 1.4.2 C3 = 0.77 for ships having two longitudinal bulkheads inside the cargo tanks extending over the length of the cargo block, and 1.0 for all other ships. In this case, there are no longitudinal bulkheads within the cargo tanks, and C3 = 1.0.

    • The mean oil outflow from side damage is therefore:

  1.5 Calculating the probabilities of bottom damage

  • 1.5.1 The first step is to determine the values for the dimensions and clearances Xa, Xf, Yp , Ys and z. Xa and Xf are as previously specified for side damage. Yp, Ys and z are defined in paragraph 9.2 of regulation 23:

    Tank Yp
    m     		Ys
    m     		z
    m
    CO1 38.000 2.000 2.000
    CO2 38.000 2.000 2.000
           

  • 1.5.2 From the ratios Xa/L, Xf/L, Yp/BB, Ys/BB, and z, the probabilities associated with these subdivision locations are interpolated from the table of probabilities for bottom damage provided in Paragraph 9.3 of regulation 23.

    Tank Xa/L PBa Xf/L PBf Yp/BB PBp Ys/BB PBs z/Ds PBz
    CO1 0.2000 0.0290 0.0290 0.8100 0.9500 0.0090 0.0500 0.0090 0.1000 0.7800
    CO2 0.3500 0.0760 0.8000 0.2520 0.9500 0.0090 0.0500 0.0090 0.1000 0.7800
                         

  • 1.5.3 In accordance with paragraph 8 of regulation 23, the probability factors are then combined to find the probability, PB, of breaching a compartment from bottom damage.

    • For tank CO1:

      PBL = (1 - PBf - PBa) = (1 - 0.810 - 0.029) = 0.161

      PBT = (1 - PBp - PBs) = (1 - 0.009 - 0.009) = 0.982

      PBV = (1 - PBz) = (1 - 0.780) = 0.220

      PB = PBL PBT PBV = (0.161)(0.982)(0.220) = 0.0348

    • For tank CO2:

      PBL = (1 - PBf - PBa) = (1 - 0.252 - 0.076) = 0.672

      PBT = (1 - PBp - PBs) = (1 - 0.009 - 0.009) = 0.982

      PBV = (1 - PBz) = (1 - 0.780) = 0.220

      PB = PBL PBT PBV = (0.161)(0.982)(0.220) = 0.1452

  • 1.5.4 Given a grounding that penetrates the outer hull, PB is the probability that the damage will extend into a particular cargo tank. As shown above, the probability of breaching the CO2 tank from bottom damage is 0.1452, or about 14.5%.

  1.6 Calculating the mean outflow from bottom damage

  • 1.6.1 For bottom damage, outflow is computed based on hydrostatic pressure balance, in accordance with the assumptions described in paragraph 7 of regulation 23. Independent calculations are performed for 0.0 m and minus 2.5 m tides, and then the results are combined to provide an overall mean outflow for bottom damage.

  • 1.6.2 Per paragraph 7.3.2 of regulation 23, the cargo level after damage, measured in metres above Zl, is calculated as follows:

    where:
    ds = the load line draught = 9.0 m
    tc = the tidal change = 0 m and -2.5 m
    Zl = the height of the lowest point in the cargo tank above baseline = 2.0 m
    ρs = density of seawater, to be taken as 1,025 kg/m3
    p = inert gas overpressure = 5 kPa
    g = acceleration of gravity = 9.81 m/s2
    ρn = nominal density of cargo oil = 900 kg/m3
    = For 0.0 m tide:
    =
    = For 2.5 m tide:
    =

  • 1.6.3 The oil outflow, OB, from each tank due to bottom damage equals the original volume (98% of tank capacity) minus the amount remaining (oil up to level hc).

      Oil Outflow (m3) at
    Tank at 0.0 m tide at -2.5 m tide
    CO1 5,471 6,993
    CO2 16,413 20,979
         

  • 1.6.4 In accordance with paragraphs 7.1 and 7.2 of regulation 23, the mean outflow from bottom damage is calculated as follows:

  • 1.6.5 It is recognized that a portion of the oil escaping from a cargo tank may be entrapped by a double bottom tank below, thereby preventing the oil from reaching the sea. In accordance with paragraph 7.4 of regulation 23, CDB(i) is to be taken as 0.6 when a cargo tank is bounded from below by a non-oil compartment.

  • 1.6.6 The mean outflow from bottom damage without tidal change is:

    Tank PB(i) OB(i) (m3) CDB(i) OMB(i) (m3)
    CO1 0.0348 5,471 0.6 114
    CO2 0.1452 16,413 0.6 1,430
          OMB(0) = 1,544

  • 1.6.7 The mean outflow after a 2.5 m reduction in tide is:

    Tank PB(i) OB(i) (m3) CDB(i) OMB(i) (m3)
    CO1 0.0348 6,993 0.6 146
    CO2 0.1452 20,979 0.6 1,828
          OMB(2.5) = 1,974

  • 1.6.8 In accordance with paragraph 5.2 of regulation 23, mean outflow values from the 0.0 m and -2.5 m tide conditions are combined in a 70%:30% ratio to obtain the bottom damage mean outflow:

    • OMB = 0.7 OMB(0) + 0.3 OMB(2.5) (m3)

      OMB = (0.7)(1,544) + (0.3)(1,974) = 1,673 m3

  1.7 Calculating the mean outflow parameter

  • 1.7.1 In accordance with paragraph 5.1 of regulation 23, the mean outflow from side damage and bottom damage are combined in a 40%:60% ratio and then this value is divided by the total oil volume C to obtain the overall mean outflow parameter:

    • OM = ( 0.4 OMS + 0.6 OMB ) / C

      OM = [(0.4)(4,172) + (0.6)(1,673)] / 3,721 = 0.071

  • 1.7.2 The final step in the evaluation of an actual oil tanker is to compare the calculated value of OM with the maximum permissible value given in paragraph 3.1 of regulation 23.

Parent topic: Part C - Examples
Copyright 2022 Clasifications Register Group Limited, International Maritime Organization, International Labour Organization or Maritime and Coastguard Agency. All rights reserved. Clasifications Register Group Limited, its affiliates and subsidiaries and their respective officers, employees or agents are, individually and collectively, referred to in this clause as 'Clasifications Register'. Clasifications Register assumes no responsibility and shall not be liable to any person for any loss, damage or expense caused by reliance on the information or advice in this document or howsoever provided, unless that person has signed a contract with the relevant Clasifications Register entity for the provision of this information or advice and in that case any responsibility or liability is exclusively on the terms and conditions set out in that contract.