3 Damage Statistics

 The following considerations are based on the information contained in various IMO documents. They summarize casualty data reported to IMO on 811 damage cards. There are 296 cases of rammed ships which contain information on each of the following characteristics:

• Ship length - L

• Ship breadth - B

• Damage location - x

• Damage length - y

• Damage penetration - z

 In order to omit inconsistencies in the results derived from the data, which may be caused by the use of different samples, the following investigations have been based only on the aforementioned 296 cases. However, further investigations have been made using, in addition, the information given for other cases. Despite the random scatter, which is to be expected because of the use of different samples composed at random, they lead to the same conclusion.

 For the investigation of the dependency of damage length on the year of collision, a different sample was used comprising 209 cases in which L, y and year of collision were given.

 It is clear that the principal factors affecting damage extent are:

• .1 structural characteristics of the rammed ship;

• .2 structural characteristics of the ramming ship;

• .3 mass of the rammed ship at time of collision;

• .4 mass of the ramming ship at time of collision;

• .5 speed of the rammed ship at time of collision;

• .6 speed of the ramming ship at time of collision;

• .7 relative course angle between rammed and ramming ship;

• .8 location of damage relative to the ship's length.

 From the point of view of the rammed ship only item .1 is pre-determined; all other items are random. An investigation of the damage length of ships with different numbers of decks has shown that there is no significant influence. This does not prove that there is no influence. It is, however, valid to conclude that the influence of structural characteristics is relatively small. It therefore seems justifiable to neglect this influence.

 The mass of the rammed ship depends on its size and its loading condition. The influence of the latter is small and therefore for the sake of simplicity it has been neglected. To account for the size of the rammed ship, damage length has been related to the ship length and damage penetration to the ship breadth.

 The following will show that the damage length does not depend significantly on the place at which it occurs in the ship's length. From this it is concluded that the damage extent does not depend on the location of the damage, except at the ends of the ship where damage length is bounded according to the definition of damage location as the centre of the damage.

 Some comments on the mass of the ramming ship are given below.

 Preliminary investigations have led to the conclusion that the distribution of the ratio damage length to ship length y/L is more or less independent of the ship length. A proof will be given below. As a consequence, y/L can be taken as independent of L.

 From theoretical considerations (using the central limit theorem) it follows that (where ∊y is constant) is approximately log-normally distributed. This is confirmed by Figures 7 and 8, in which good agreement is shown between the log-normal distribution function and distribution density on the one hand and the corresponding results of the damage statistics on the other.

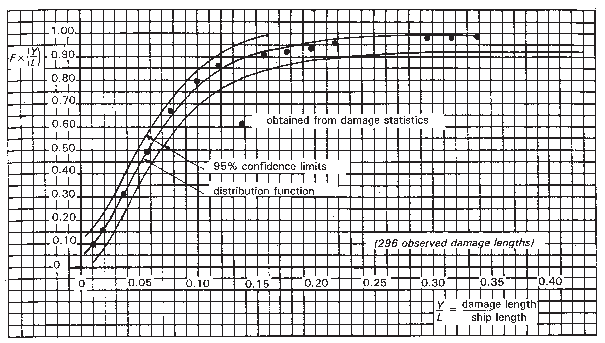
Figure 7 Distribution function of non-dimensional damage length

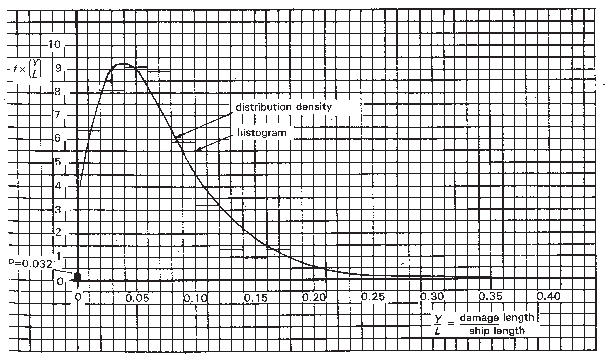
Figure 8 Distribution density of non-dimensional damage length

  Figure 9 shows the regression of y/ L on L for L≤200 m (five damages relate to ships with L>200 m). The regression line has a small negative slope which proved to be insignificant, and may be caused by samples taken at random. There might be a small dependence of y/L on the ship length, but it is so small that it cannot be derived from the given sample. It is therefore certainly no significant error to assume y/L to be independent of ship size for L≤200 m.

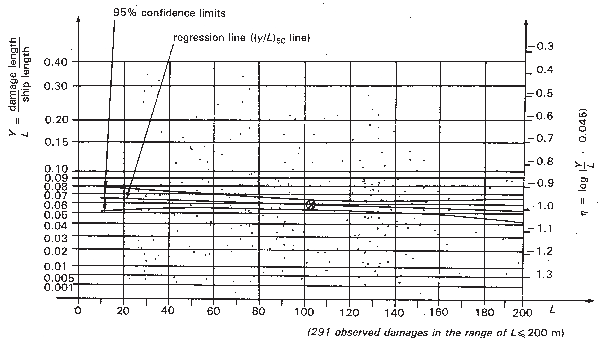
Figure 9 Regression of non-dimensional damage length on ship length

 An explanation of this independence might be that small vessels are more likely to meet mainly small vessels and large vessels are more likely to meet mainly large vessels. However, this reasoning cannot be extended to very large vessels because of the small total number of such ships. Because of the very few damage cases concerning ships with L>200 m, nothing can be said about the damage distribution of such ships. It seems reasonable to assume, as an approximation for ships with L> 200 m, that the median of the damage length is constant and equal to the median for L = 200 m. The latter equals 200 x (y/L)₅₀ where (y/L)₅₀ is the median of the non-dimensional damage length for ships with L = 200 m.

 The regression of the non-dimensional damage length y/L on the non-dimensional damage location is given in Figure 10. This shows that there is no significant difference between the damage distributions in the forward and aft half of the ship, but simple geometric reasoning indicates that the damage length at the ends of the ship - forward as well as aft - is limited to smaller values than in the central part of the ship. Therefore the log-normal distribution found for all values for y/L - independent of damage location - is the marginal distribution. The corresponding conditional distribution of y/L, on the condition that the damage location is given, does not need to be considered as for the practical application an approximation will be used, which allows establishment of a very simple relationship between the conditional and marginal damage length distribution.

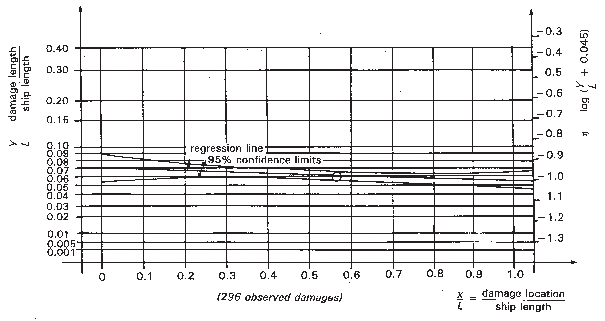
Figure 10 Regression of non-dimensional damage length on non-dimensional damage location

 The fact that the speed and size of ships has tended to increase during recent years suggests that the average size of damage in cases of collision is also growing. In order to investigate this, a regression analysis of the logarithm of the non-dimensional damage length on the year of collision has been made. The result is shown in Figure 11. This figure shows a significant positive slope of the regression line, which proves that, on average, the damage length increases with year of collision.

Figure 11 Regression of non-dimensional damage length depending on year of collision

 It therefore seems prudent not to use the distribution which results from all damage data independent of the year of collision. Assuming that the variance about the regression line is constant, it is possible to derive from the regression analysis the distribution function of non-dimensional damage length for any arbitrarily chosen year; such a function is determined by the mean (which is given by the regression line) and the variance about the regression line of the logarithm of . Some samples are given in Figures 12 and 13.

Figure 12 Distribution function of non-dimensional damage length for respective year of collision

Figure 13 Distribution density of non-dimensional damage length for respective year of collision

 Similar considerations as in the case of the damage length lead to the conclusion that is approximately log-normally distributed and does not depend on the ship size, which in this connection is represented by the breadth B of the ship. Figures 14 and 15 show good agreement between the log-normal distribution and the corresponding values obtained from the damage statistics. Figure 16 proves that there is, in fact, no significant dependence of z/B on B.

Figure 14 Distribution function of non-dimensional damage penetration

Figure 15 Distribution density of non-dimensional damage penetration

Figure 16 Regression of non-dimensional damage penetration on ship breadth

 As is to be expected, there is a strong correlation between z/B and y/ L. Figures 17 and 18 show that z/B increases on the average with increasing y/L. The joint distribution of the logarithm of () and () is a bivariate normal distribution. From that distribution the conditional distribution of z/B, on the condition that the damage length assumes certain values of y/L, can be derived.

Figure 17 Regression of non-dimensional damage penetration on non-dimensional damage length

Figure 18 Mean and median of conditional distribution of non-dimensional damage penetrationon non-dimensional damage length

 Inspection of the histogram (Figure 19) of the non-dimensional damage location shows that damages in the forward half of the ship are more frequent than in the aft part. The only explanation which can be offered for the peaks of the histogram at approximately x/L = 0.45 and x/L = 0.95 is that they are random because of the limited sample.

Figure 19 Distribution density of non-dimensional damage location

 Because the damage location is defined as distance from the aft terminal of L to the centre of the damage, it is always at a distance of y/2L from the ends of the ship. Starting with a simple assumption for the conditional distribution of x/L on the condition that y/L assumes certain values, the marginal distribution density has been derived and is shown as a curve in Figure 19. The corresponding distribution function is given in Figure 20.

Figure 20 Distribution function of non-dimensional damage location