1.1 Hull-borne mode
Clasification Society 2024 - Version 9.40
Statutory Documents - IMO Publications and Documents - International Codes - DSC Code - Code of Safety for Dynamically Supported Craft – Resolution A.373(X) - Appendix II - Methods Relating to the Intact Stability Investigation of Hydrofoil Boats - 1. Surface piercing hydrofoils - 1.1 Hull-borne mode

1.1 Hull-borne mode

  1.1.1 The stability should be sufficient to satisfy 2.3 and 2.4 of this Code.

  1.1.2 Heeling moment due to turning

The heeling moment developed during manoeuvring of the craft in the displacement mode may be derived from the following formula:

where
MR = moment of heeling;
Vo = speed of the craft in the turn (metres per second);
Δ = displacement (tonnes);
L = length of the craft on the waterline (metres);
KG = height of the centre of gravity above keel (metres).

This formula is applicable when the ratio of the radius of the turning circle to the length of the craft is 2 to 4.

  1.1.3 Relationship between the Capsizing Moment and Heeling Moment to satisfy the weather criterion

The stability of a hydrofoil boat in the displacement mode can be checked for compliance with the weather criterion K as follows:

where

  • Mc - minimum capsizing moment as determined when account is taken of rolling:
  • Mv - dynamically applied heeling moment due to the wind pressure.

  1.1.4 Heeling Moment due to Wind Pressure

The heeling moment Mv is a product of wind pressure Pv the windage area Av and the lever of windage area Z.

The value of the heeling moment is taken as constant during the whole period of heeling.

The windage area Av is considered to include the projections of the lateral surfaces of the hull, superstructure and various structures above the waterline. The windage area lever Z is the vertical distance to the centre of windage from the waterline and the position of the centre of windage maybe taken as the centre of the area.

The values of the wind pressure in Pascal associated with Force 7 Beaufort Scale depending on the position of the centre of windage area are given in Table 1.

Table 1 Typical Wind Pressures for Beaufort Scale 7 - 100 Nautical Miles from Land

Z above waterline (metres) 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0
Pv (Pascal) 46 46 50 53 56 58 60 62 64

Note: These values may not be applicable in all areas.

  1.1.5 Evaluation of the Minimum Capsizing Moment Mc in the displacement mode

The minimum capsizing moment is determined from the static and dynamic stability curves taking rolling into account.

  • (a) When the static stability curve is used, MC is determined by equating the areas under the curves of the capsizing and righting moments (or levers) taking rolling into account - as indicated by Figure 1, where θz, is the amplitude of roll and MK is a line drawn parallel to the abscissa axis such that the shaded areas S1 and S2 are equal.

    Mc = OM if the scale of ordinates represents moments
    Mc = OM × Displacement if the scale of ordinates represents levers

  • (b) When the dynamic stability curve is used, first an auxiliary point A must be determined. For this purpose the amplitude of heeling is plotted to the right along the abscissa axis and a point A' is found (see Figure 2). A line AA' is drawn parallel to the abscissa axis equal to the double amplitude of heeling (AA'=2θz) and the required auxiliary point A is found. A tangent AC to the dynamic stability curve is drawn. From the point A the line AB is drawn parallel to the abscissa axis and equal to 1 radian (57.3°). From the point B a perpendicular is drawn to intersect with the tangent in point E. The distance is equal to the capsizing moment if measured along the ordinate axis of the dynamic stability curve. If, however, the dynamic stability levers are plotted along this axis is then the capsizing lever, and in this case the capsizing moment Mc is determined by multiplication of ordinate in metres by the corresponding displacement in tonnes

    Mc = 9.81 Δ (Kilonewton-metres)

  • (c) The amplitude of rolling θz, is determined by means of model and full-scale tests in irregular seas as a maximum amplitude of rolling of 50 oscillations of a craft travelling at 90° to the wave direction in sea state for the worst design condition. If such data are lacking the amplitude is assumed to be equal to 15°.

  • (d) The effectiveness of the stability curves should be limited to the angle of flooding.

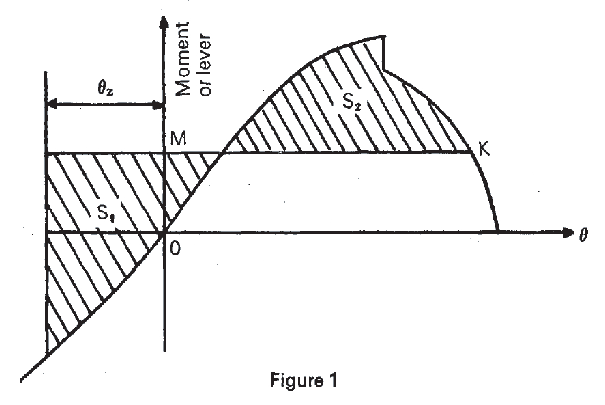
Figure 1 Static Stability Curve

Figure 2 Dynamic Stability Curve

Parent topic: 1. Surface piercing hydrofoils
Copyright 2022 Clasifications Register Group Limited, International Maritime Organization, International Labour Organization or Maritime and Coastguard Agency. All rights reserved. Clasifications Register Group Limited, its affiliates and subsidiaries and their respective officers, employees or agents are, individually and collectively, referred to in this clause as 'Clasifications Register'. Clasifications Register assumes no responsibility and shall not be liable to any person for any loss, damage or expense caused by reliance on the information or advice in this document or howsoever provided, unless that person has signed a contract with the relevant Clasifications Register entity for the provision of this information or advice and in that case any responsibility or liability is exclusively on the terms and conditions set out in that contract.